|
 3D Engine 2 - matrices and transformations 
Hi ! I'm back again. Today we'll fix on matrix stuff and then write our first 3D-engine.
What the matrix is ? It's math expression for two-dimensional array of numbers. (exactly,
it's array of vectors, because vector is array of elements, but i will always mean three
coordinates, meaning direction by vector) Common matrix :
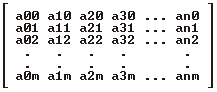
We would write this matrix as a nm, where m, n are dimensions of our matrix. We
will need matrix of fourth order, and we will want to be accurate so we will use floats
for it. Why not double ? We need to be able to express very small and very large numbers
so we can't afford ussage of number with fixed point :
typedef float Matrix[4][4];
|
Well, we have our matrix. But what does it mean ? What is inside and what do do with it ?
Inside there are four vectors. First three are pointing "right", "up" and "forward" - so they
express our local coordinate system (right is x, up y and forward z - coordinate) The fourth
vector points at our local origin. They are placed in upper three rows of matrices, first
column is right, second up, third forward and fourth is position. (i can tell that first line
will be it's x - coordinate, second line is y and third one is z.) Now, we should be able
to write some code for transformation of vertex by matrix :
tx = x * m[0][0] + y * m[1][0] + z * m[2][0] + m[3][0]
ty = x * m[0][1] + y * m[1][1] + z * m[2][1] + m[3][1]
tz = x * m[0][2] + y * m[1][2] + z * m[2][2] + m[3][2]
|
I think it's obvious that x, y, z is our vertex, tx, ty, tz is transformed vertex, m is our
transformation matrix. Firs bracket contains column, second row - exactly like in OpenGL (conversely to Direct3D). You can see only three
rows are used. What's in the fourth one ? There will always be [0 0 0 1]. Why that ?
We will see in the moment - with matrix with the same count of rows and columns you can
do much more operations. There were systems that had just three rows and fourth one
was added when computing something, but it's only complicated. Now, it's time to introduce
the unit matrix. It's the matrix, having ones in the main diagonal and zeros in other
positions :
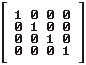
When matrix is unit, you can see that local origin is [0 0 0], right is [1 0 0], up [0 1 0]
and forward [0 0 1] - that's the original state. Well, we have our first function :
void Matrix_Init(Matrix *m)
{
int i, j;
for(i = 0; i < 4; i ++)
for(j = 0; j < 4; j ++)
(*m)[i][j] = (float)(i == j);
}
|
Maybe you wonder what kind of entry this is, but it's quite allright in C. When i is
equal to j, the result will be 1, otherwise 0. Rest of the function should be self-explanatroy.
Right, so we have our objects in their initial positions, but what about some movement ?
Maybe you find out that you can translate object in world-space by adding translation
vector coordinates to local origin ( m[3][0], m[3][1], m[3][2]) and that would be allright.
But it would be more useful to translate it in object-space. It can be done by adding
transformed translation vector (vector - i.e. direction, not position - transformation
code is similar to transformation code above, but you won't add local origin position)
or by multiplying our matrix by unit matrix with filled translation. You can find in any
math book way to multiply matrices :
void Matrix_Multiply(Matrix *a, Matrix *b, Matrix *r)
{
Matrix temp;
int i, j;
for(i = 0; i < 4; i ++) {
for(j = 0; j < 4; j ++)
temp[i][j] = (*a)[0][j] * (*b)[i][0] + (*a)[1][j] * (*b)[i][1] +
(*a)[2][j] * (*b)[i][2] + (*a)[3][j] * (*b)[i][3];
}
memcpy(r, temp, sizeof(Matrix));
}
|
It's quite simple, isn't it ? Yes, maybe when seen first time it's not. But here is our
translation code waiting :
void Matrix_Translate(Matrix * m, float dx, float dy, float dz)
{
Matrix temp;
Matrix_Init(&temp);
temp[3][0] = dx;
temp[3][1] = dy;
temp[3][2] = dz;
Matrix_Multiply(m, &temp, m);
}
|
It's exactly as i told you - unit matrix, fill translation and multiply. Rotation is quite
the same. The matrices, used to multiply our object matrix have modified right, up and
forward vectors, according to desitred rotation. This is now simple rotation of unit
vector arround origin. Let's see our code :
void Matrix_Rotate_X(Matrix *m, float angle)
{
Matrix temp;
Matrix_Init(&temp);
temp[2][1] = (float)-sin(angle);
temp[2][2] = (float)cos(angle);
temp[1][1] = (float)cos(angle);
temp[1][2] = (float)sin(angle);
Matrix_Multiply(m, &temp, m);
}
void Matrix_Rotate_Y(Matrix *m, float angle)
{
Matrix temp;
Matrix_Init(&temp);
temp[0][0] = (float)cos(angle);
temp[0][2] = (float)-sin(angle);
temp[2][2] = (float)cos(angle);
temp[2][0] = (float)sin(angle);
Matrix_Multiply(m, &temp, m);
}
void Matrix_Rotate_Z(Matrix *m, float angle)
{
Matrix temp;
Matrix_Init(&temp);
temp[0][0] = (float)cos(angle);
temp[0][1] = (float)sin(angle);
temp[1][1] = (float)cos(angle);
temp[1][0] = (float)-sin(angle);
Matrix_Multiply(m, &temp, m);
}
|
Well, that's it. Now we can move with objects, camera, can transform vertices so we can draw
- or not ? Last time i told you it's not necessary to transform objects to wolrdspace
and then to cameraspace. There is direct transformation from objectspace to cameraspace.
What do we need ? You take camera matrix, invert it (mathematical operatiop), transpond
it (switch rows to columns) and with the result simply multiply object matrix. We will
connect inversion and transponding (somebody tell me how is this word correct !) into single
function. Inverse matrix is computed by taking determinant (number) of whole matrix and
subdeterminants for every item in matrix (it's actually determinant of matrix, when you
leave out row and column the respective item is lying). You multiply each subdeterminant
by (row + column)th power of -1 and divide by determinant of whole matrix. We can do
optimalisation, because we know that last row of matrix will be again [0 0 0 1] ...
I should remind result of multiplication of matrix with it's inverse matrix will be unit
matrix :-0 ! So, don't forget code is working for matrices with last row [0 0 0 1]
and it's not only inversion, but also transponent :
void Matrix_Inverse(Matrix *src, Matrix *inv)
{
float f_det;
int i, j;
f_det = (*src)[0][0] * (*src)[1][1] * (*src)[2][2] +
(*src)[1][0] * (*src)[2][1] * (*src)[0][2] +
(*src)[0][1] * (*src)[1][2] * (*src)[2][0] -
(*src)[0][2] * (*src)[1][1] * (*src)[2][0] -
(*src)[0][1] * (*src)[1][0] * (*src)[2][2] -
(*src)[0][0] * (*src)[1][2] * (*src)[2][1];
(*inv)[0][0] = (*src)[1][1] * (*src)[2][2] -(*src)[1][2] * (*src)[2][1] ; (*inv)[1][0] =-(*src)[1][0] * (*src)[2][2] +(*src)[1][2] * (*src)[2][0] ; (*inv)[2][0] = (*src)[1][0] * (*src)[2][1] -(*src)[1][1] * (*src)[2][0] ; (*inv)[3][0] =-(*src)[1][0] * (*src)[2][1] * (*src)[3][2] -
(*src)[1][1] * (*src)[2][2] * (*src)[3][0] -
(*src)[2][0] * (*src)[3][1] * (*src)[1][2] +
(*src)[1][2] * (*src)[2][1] * (*src)[3][0] +
(*src)[1][1] * (*src)[2][0] * (*src)[3][2] +
(*src)[2][2] * (*src)[1][0] * (*src)[3][1];
(*inv)[0][1] =-(*src)[0][1] * (*src)[2][2] + (*src)[0][2] * (*src)[2][1];
(*inv)[1][1] = (*src)[0][0] * (*src)[2][2] - (*src)[0][2] * (*src)[2][0];
(*inv)[2][1] =-(*src)[0][0] * (*src)[2][1] + (*src)[0][1] * (*src)[2][0];
(*inv)[3][1] = (*src)[0][0] * (*src)[2][1] * (*src)[3][2] +
(*src)[0][1] * (*src)[2][2] * (*src)[3][0] +
(*src)[2][0] * (*src)[3][1] * (*src)[0][2] -
(*src)[0][2] * (*src)[2][1] * (*src)[3][0] -
(*src)[0][1] * (*src)[2][0] * (*src)[3][2] -
(*src)[2][2] * (*src)[0][0] * (*src)[3][1];
(*inv)[0][2] = (*src)[0][1] * (*src)[1][2] - (*src)[0][2] * (*src)[1][1];
(*inv)[1][2] =-(*src)[0][0] * (*src)[1][2] + (*src)[0][2] * (*src)[1][0];
(*inv)[2][2] = (*src)[0][0] * (*src)[1][1] - (*src)[0][1] * (*src)[1][0];
(*inv)[3][2] =-(*src)[0][0] * (*src)[1][1] * (*src)[3][2] -
(*src)[0][1] * (*src)[1][2] * (*src)[3][0] -
(*src)[1][0] * (*src)[3][1] * (*src)[0][2] +
(*src)[0][2] * (*src)[1][1] * (*src)[3][0] +
(*src)[0][1] * (*src)[1][0] * (*src)[3][2] +
(*src)[1][2] * (*src)[0][0] * (*src)[3][1];
for(j = 0; j < 4; j ++)
for(i = 0; i < 3; i ++)
(*inv)[j][i] /= f_det;
(*inv)[0][3] = 0;
(*inv)[1][3] = 0;
(*inv)[2][3] = 0;
(*inv)[3][3] = 1;
}
|
That's it. For the sake of clarify - Sarrus's rule is rule for computing determinants,
works for matrices up to order of 3. You simply multiply numbers in diagonals going
down and right and substract multiplied numbers in diagonals going down and left.
(now neither do i understand it ... please find it in your math book or at math.com)
If you'r memory is good - you will remember we have to do perspective correction in order
to draw. We need perspective distortion constant. For 320 per 200 resolution it will be
320 for 45 degree angle. The angle is so called field of view. Cameras have field of view
arround 30°, quake3 90° and for example sniper rifle - mode would be arround 20° or
alliens - vision like 150° ... Maybe you remember binoculars or microscope are working
with view angle ! You can compute our constant from angle by this formula :
z_delta = n_Width / (tan(psi / 2) * 2);
Where n_Width is width of our image and psi is field of view (propably in radians).
You can deduce it from similar triangles. I will now write our first engine :
struct Vertex {
float x, y, z;
};
struct Object{
int n_vertex_num;
Vertex *vertex;
Matrix m_object;
};
void Draw_Object(Object *p_object, Matrix *p_camera)
{
float tx, ty, tz;
float x, y, z;
MATRIX m;
int i;
invertmatrix(p_camera, &m);
matmult(&m, &p_object->m_object, &m);
for(i = 0; i < p_object->n_vertex_num; i ++) {
x = p_object->vertex[i].x;
y = p_object->vertex[i].y;
z = p_object->vertex[i].z;
tx = x * m[0][0] + y * m[1][0] + z * m[2][0] + m[3][0];
ty = x * m[0][1] + y * m[1][1] + z * m[2][1] + m[3][1];
tz = x * m[0][2] + y * m[1][2] + z * m[2][2] + m[3][2];
if(tz > 0.1) { tx = (320 / 2) + (tx * z_delta) / tz;
ty = (200 / 2) + (ty * z_delta) / tz;
if(tx > 0 && tx < 320 && ty > 0 && ty < 200) {
Draw_Point(tx, ty);
} }
}
}
|
Now we can write simplifistic engine, displaying dots of some object. We need some graphical
device, for start we will use windows gdi. We also need some format to get our objects from.
Today we will use ASC format from 3d-studio (maybe milkshape can do that)
It's simple format where everythink is saved as text. You can view it in notepad.
Next time i will use more advanced format (.3ds) and DirectX. But for now you can
download sources for first engine :
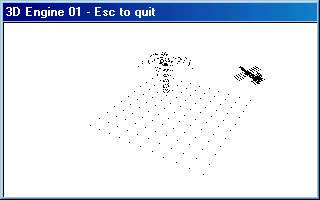
3D engine 01
-tHE SWINe-

Valid HTML 4.01
|
 3D Engine 2 - matrices and transformations
3D Engine 2 - matrices and transformations 
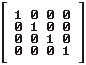

 3D engine 01
3D engine 01



