Czech Welcome Guff Coding 3D - Engine Guestbook Links Downloads About author Mail me Mailform
 3D Engine 6 - BSP-Trees
3D Engine 6 - BSP-Trees 
Hi ! I don't know what to tell you ... wait ... welcome to our great 3d show ! That was terrible.
Doesn't matter ... So i hope you liked previous part about z-buffer and texturing ... So today
we'll have look at BSP - trees.
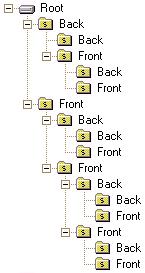
What's such tree ? BSP extends to Binary Space Partition (trees). The word binary means two. So each space is divided into two sub-spaces. How ? By a plane. When you try connect it with tree, you find it quite useful. We have root (whole space), it has two nodes (front and back subspace) and each node ... Here is some directory structure, looking like BSP (i had to format my harddisc. well, i didn't have to, but i did, because i like you ... ;P)) :
Now i should tell you how to create such a tree ...
Growing BSP-Tree
It's simple i told you you have to subdivide space into two halfs by some plane. What plane should that be ? It should be such a plane to make tree as small as possible. You should know that subdivision proceeds until the subspace is empty (ie. all polygons are lying on subdividing planes in their respective subspace) So it should cut as few polygons as possible and it should divide them approximately in half (unbalanced tree would be bigger) A real-life situation :
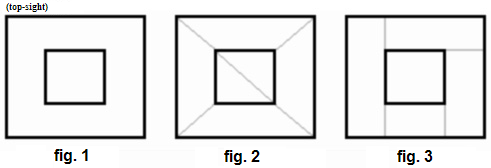
On fig.1 there's our 2D room with pillar. Fig.2 shows same room, ideally subdivided - no surfaces are split and tree is quite small. (every surface is in one subspace and lying on it's own plane) Fig.3 shows situation that should possibly generate our algorithm (we are going to design it) You can see it will try to find such a surface (= face / polygon), whose plane seems to be best splitting plane. It will split some polygons, but it will be still a very good sollution. It would be nearly impossible to try every possible plane, because each world would contain quite a lot of them (ok, not every plane, but every plane, defined by some three vertices of the world ...) Now we have to write some algorithm for finding our splitting polygon.
Split polygon selection
You see what we need to do. I already said tree must be balanced and we should reduce polygon splitting. We will simply make a loop, going over each face in our subspace and count faces that would be split by it's plane and faces, lying in front and behind that plane. Then create some score from these values and simply select the best face :
We used also two constants, that tells us importance of balance hint and reduce-split hint. Polygon with the smallest score is the winner and his plane will be used for splitting his subspace. In that process all faces lying on dividing plane (including the winner) will be put into onplane list and the rest will be divided into two (front and back) subspaces.
Dividing face
We have been already doing it in clipping pyramid, but the result was polygon. We need the result to be face. It's actualy simpler than you may think :
So, we have our Vertex and Face. But next is a Face_List - that will be structure holding list of faces (actually pointers to faces - when list grows, program call realloc and array pointer change - so this is the way to keep these pointers constant) and Vertex_List is the same. Function IntEdgePlane() computes intersection of segment, given by vertices p_v1 and p_v2 with plane p_plane. And finally in SplitPolygon() function is face p_face split (or not split when it actually doesn't intersect plane) by plane p_plane into three faces. Next parameters are front and back facelists for storing results. Algorithm simply gets numbers of vertices on each side of plane in order to classify face position and remember last front and last back vertex index. There is always one vertex lying on one side of plane and the other two on the other side of plane, so the alone vertex is always remembered as the last one. Next, the intersections are computed (based on vertices positions we know where should it lie) and new faces created (and added to list)
Creating tree itself
We should know everything to create our tree. Suppose vertices with x, y, z, u and v coordinate. (u and v are for textures) Vertices will be in one global list and faces in the other one. Every face has it's texture and precomputed plane. This all will be in root of the tree. What next do we need ? As i mentioned we should find splitting plane and then ... New nodes. We will determine from counts of faces lying in front of and behind the splitting plane if there will be any nodes and if they will, allocate memory for them. Next we take our facelist and one by one split faces nicely between nodes. New vertices, originated when splitting face are added into glogal vertex-list. (don't forget about u, v coordinates !) So we have faces split into two nodes, but what with the faces, lying onplane ? I mentioned this situation aswell. These faces will be added into an onplane list (that's his name). And that list will remain in our current node (or root) Now retype it to C. Begin with structures :
We will slowly go over them. Constants _Front, _Back, _Split and _OnPlane are returned by function, classifying face / plane position. Next _Have_Front_Node and _Have_Back_Node are used in BSP_Node::flags and marks if node has one, the other one or both nodes (they actually are used as masks) BSP_Material is material, for now it's only texture name. That should be new for you, but we need some kind of records on texture names, because bsp file will be standalone thus we cannot load them later from original (source) .3ds file. BSP_Node is node of the tree here is flags i mentioned above (0 - no children, 1 - has front node, 2 - has back node, 3 - both nodes). Next there are pointers to front and back child - node, plane rootpl of face, selected as splitting face and then lists of faces (face contain all face in node itself and it's subnodes and onplane contain onplane faces) and pointer to global vertexlist. (BSP_Tree::vertex) And BSP_Tree contain complete tree, that are global lists of geomethry (ie. vertices and faces), pointer to root node (node containing all faces) and list of materials we will need for texturemapping in future. We will start creating tree from 3ds-world :
It's code, preparing the root of the tree. Every data structure is copied (vertices should be transformated by it's object matrices since BSP-tree will be static and it will be in fact single object) Also memory for first node (root) is allocated. The global variables are current height of tree, maximal achieved height of tree, number of faces, number of processed faces and number of processed nodes. You should already know all the macros, aparts from _Epsilon, that's maximal variance that is taken as zero (mainly for classifying face (vertex) / plane position) Yes - and the strange characters 'Ì', 'È', 'Í' are dos graphic characters, you'll see it in console. Now some interesting stuff :
At the beggining is done some level computing, then memory for subnodes is allocated (as process goes trough, the info on what's current level, polygon and node counts is plotted onto the screen) Then splitting plane is found, if result is -1, it means node is convex, so next subdividing is useless (convex means all faces are lying on one side of the other's faces planes - that's a bit bad told - simply when you would create next nodes, for example the front ones would be always empty and in the back ones would be always one face less - imagine BSP for sphere) Next function PartitionSpace() is called to split polygons between subnodes. After that, subnodes (if some) are recursively created. Now describe FindRootPoly()
First UpdateStatus() - function for printing rotating dash (since creating tree can last quite long it's good to know if it's stuck or it's doing something) Next there are simple functions for classifying vertex (face) relative position to plane. Function FindRootPoly() itself counts polygons on all sides of plane and the ones to split. At the same time add results to total sums of polygons, helping to tell if node is convex (it's convex if all polygons are lying on one side and there are no splits) It actually will be convex or concave or none of that. It depends on direction we want to draw (front-to-back or back-to-front) which one we allow to skip creating next node - so it will be necessary to modify this part ! Then actual score is computed, compared with the previous one and sometimes updated. Then do rotating dash. On the end of function, convexity test is made and -1 or splitting face index is returned. This will be propably the slowest possible way to find splitting face.
I know one more method for doing that - it was invented by Paul Nettle aka. Midnight (hope i'm not wrong). The face planes are put into so called gauss map (groups, divided by normal and sorted by prependicular distance from zero) and then in each group the plane with best balance is found. (since planes are sorted, you can use quick algorithm of interval halving or another name Newton search) From these best planes the one with fewest splits is selected as splitting plane. It will be quite faster, but it assumes some faces have the same normal vector (ie. parallel planes), but when considering common quake level, most of surfaces are prependicular to itself.
But back to our algorithm. Now we're missing only PartitionSpace() :
On the beginning the facelists are set clear, flags is set to zero (no subnodes) and faces are subdivided into their respective facelists. At the same time, flags are updated. It's simple.
I won't tell you how does facelists work, because it's really simple aswell as file writing / loading routines. If you find something difficult, just mail me or get some book about C.
By now, we should have everything we need to write the very basic BSP-compiller. You can download source codes, compille exe and watch the spinning dash ! (when debugging my first BSP, i even dreamed about it !)
 BSP Compiller
BSP Compiller

Basic BSP tree ussage
If you are keen on games, you may know that lots of games are using BSP's. But it's a bit different (but offen) way than we will do today. We will use BSP-tree for sorting surfaces in order to be drawn correctly. For example Quake, Unreal or Half-life are using precomputed visibility sets (PVS) The BSP is taken to generate convex zones. Based on spawnpoint locations (that's where player is born) select zones where player can reach. From the other ones remove all the geometry (this part is called hidden surface removal, guess why ...) Then for each zone take all possible viewing points and determine which other zones are visible from it. So when drawing, you almost exactly knows that all of the faces you draw will be visible. This is ideal, because it elliminates overdraw so we can use Z-buffer. (almost all older games (Quake I, Unreal I and Half-life I) were using S-buffer as I'm going to tell you in next part) But there is one more way to use BSP tree. For example Descent (I, II) used portal - based rendering. You generate zones again, but you don't compute PVS, but create potrals. They're areas, connecting zones so when rendering, the area (and it's contents) containing camera was drawn. Then visible portal was taken and next area was drawn recursively, but clipped by that portal's edges. This method will make zero overdraw (assuming only BSP is drawn - ie. no objects, etc ...), but it's hard to make hardware accelerated (ok, i could use stencil buffer and clipping planes, but PVS will be faster - and simpler)
Now back to our source again. So we will use it to sort surfaces. When drawing with Z-buffer, we could only check if something was drawn before (it will be more likely C - coverage buffer) and when screen is full we can stop drawing. That's not bad, but for now we will show only simple BSP traversal :
That was the very basic ussage of BSP. It will draw polygons back to front. If you'd like to switch the order, you will have to swap order of sub-node drawing in both branches (or invert the condition) The rest will be just like paither's algorithm : clip, transform, rasterize. I won't go deeper now since you should be able to understand that. Here is source for BSP - engine :

 BSP Engine
BSP Engine

Positives and negatives of BSP
The certain disadvantage is polygon overdraw. Next disadvantage is that world is static. Moving things can't be part of BSP. So what did it bring us ? We can tell where camera is very fast and we can do very fast raytracing. That's all - if you have pure BSP, but when using portals or PVS, it will be significant boost. It could be also used with some algorithm for visibility determination (hardware Z-buffer or S-buffer / C-buffer) for more speed-up. Something on S-Buffer in next part ...
Variants of BSP
We just described BSP-trees, but it's not the only sort of spatial subdivision. Very common are OcTrees (Octal) - world is in cube, it will have eight sub-cubes (divided in half by x, y and z - axis) That is useful when world doesn't contain any good surfaces for splitting (for example terrain ...) There are KD-trees, they are just like BSP, but dividing planes will be always prependicular to one of coordinate axes (x, y / z).
For BSP-trees - today we used BSP - tree with onplane lists, but for PVS is used so called leaf BSP. It focuses on faces inside of node, not just onplanelists. But more on that later when writing some PVS based OpenGL engine ... bye !
Yes, people - write your opinion about pages, my terrible english ... Should i translate also comments in source codes ??
-tHE SWINe-
What's such tree ? BSP extends to Binary Space Partition (trees). The word binary means two. So each space is divided into two sub-spaces. How ? By a plane. When you try connect it with tree, you find it quite useful. We have root (whole space), it has two nodes (front and back subspace) and each node ... Here is some directory structure, looking like BSP (i had to format my harddisc. well, i didn't have to, but i did, because i like you ... ;P)) :

Now i should tell you how to create such a tree ...
Growing BSP-Tree
It's simple i told you you have to subdivide space into two halfs by some plane. What plane should that be ? It should be such a plane to make tree as small as possible. You should know that subdivision proceeds until the subspace is empty (ie. all polygons are lying on subdividing planes in their respective subspace) So it should cut as few polygons as possible and it should divide them approximately in half (unbalanced tree would be bigger) A real-life situation :

On fig.1 there's our 2D room with pillar. Fig.2 shows same room, ideally subdivided - no surfaces are split and tree is quite small. (every surface is in one subspace and lying on it's own plane) Fig.3 shows situation that should possibly generate our algorithm (we are going to design it) You can see it will try to find such a surface (= face / polygon), whose plane seems to be best splitting plane. It will split some polygons, but it will be still a very good sollution. It would be nearly impossible to try every possible plane, because each world would contain quite a lot of them (ok, not every plane, but every plane, defined by some three vertices of the world ...) Now we have to write some algorithm for finding our splitting polygon.
Split polygon selection
You see what we need to do. I already said tree must be balanced and we should reduce polygon splitting. We will simply make a loop, going over each face in our subspace and count faces that would be split by it's plane and faces, lying in front and behind that plane. Then create some score from these values and simply select the best face :
|
We used also two constants, that tells us importance of balance hint and reduce-split hint. Polygon with the smallest score is the winner and his plane will be used for splitting his subspace. In that process all faces lying on dividing plane (including the winner) will be put into onplane list and the rest will be divided into two (front and back) subspaces.
Dividing face
We have been already doing it in clipping pyramid, but the result was polygon. We need the result to be face. It's actualy simpler than you may think :
|
So, we have our Vertex and Face. But next is a Face_List - that will be structure holding list of faces (actually pointers to faces - when list grows, program call realloc and array pointer change - so this is the way to keep these pointers constant) and Vertex_List is the same. Function IntEdgePlane() computes intersection of segment, given by vertices p_v1 and p_v2 with plane p_plane. And finally in SplitPolygon() function is face p_face split (or not split when it actually doesn't intersect plane) by plane p_plane into three faces. Next parameters are front and back facelists for storing results. Algorithm simply gets numbers of vertices on each side of plane in order to classify face position and remember last front and last back vertex index. There is always one vertex lying on one side of plane and the other two on the other side of plane, so the alone vertex is always remembered as the last one. Next, the intersections are computed (based on vertices positions we know where should it lie) and new faces created (and added to list)
Creating tree itself
We should know everything to create our tree. Suppose vertices with x, y, z, u and v coordinate. (u and v are for textures) Vertices will be in one global list and faces in the other one. Every face has it's texture and precomputed plane. This all will be in root of the tree. What next do we need ? As i mentioned we should find splitting plane and then ... New nodes. We will determine from counts of faces lying in front of and behind the splitting plane if there will be any nodes and if they will, allocate memory for them. Next we take our facelist and one by one split faces nicely between nodes. New vertices, originated when splitting face are added into glogal vertex-list. (don't forget about u, v coordinates !) So we have faces split into two nodes, but what with the faces, lying onplane ? I mentioned this situation aswell. These faces will be added into an onplane list (that's his name). And that list will remain in our current node (or root) Now retype it to C. Begin with structures :
|
We will slowly go over them. Constants _Front, _Back, _Split and _OnPlane are returned by function, classifying face / plane position. Next _Have_Front_Node and _Have_Back_Node are used in BSP_Node::flags and marks if node has one, the other one or both nodes (they actually are used as masks) BSP_Material is material, for now it's only texture name. That should be new for you, but we need some kind of records on texture names, because bsp file will be standalone thus we cannot load them later from original (source) .3ds file. BSP_Node is node of the tree here is flags i mentioned above (0 - no children, 1 - has front node, 2 - has back node, 3 - both nodes). Next there are pointers to front and back child - node, plane rootpl of face, selected as splitting face and then lists of faces (face contain all face in node itself and it's subnodes and onplane contain onplane faces) and pointer to global vertexlist. (BSP_Tree::vertex) And BSP_Tree contain complete tree, that are global lists of geomethry (ie. vertices and faces), pointer to root node (node containing all faces) and list of materials we will need for texturemapping in future. We will start creating tree from 3ds-world :
|
It's code, preparing the root of the tree. Every data structure is copied (vertices should be transformated by it's object matrices since BSP-tree will be static and it will be in fact single object) Also memory for first node (root) is allocated. The global variables are current height of tree, maximal achieved height of tree, number of faces, number of processed faces and number of processed nodes. You should already know all the macros, aparts from _Epsilon, that's maximal variance that is taken as zero (mainly for classifying face (vertex) / plane position) Yes - and the strange characters 'Ì', 'È', 'Í' are dos graphic characters, you'll see it in console. Now some interesting stuff :
|
At the beggining is done some level computing, then memory for subnodes is allocated (as process goes trough, the info on what's current level, polygon and node counts is plotted onto the screen) Then splitting plane is found, if result is -1, it means node is convex, so next subdividing is useless (convex means all faces are lying on one side of the other's faces planes - that's a bit bad told - simply when you would create next nodes, for example the front ones would be always empty and in the back ones would be always one face less - imagine BSP for sphere) Next function PartitionSpace() is called to split polygons between subnodes. After that, subnodes (if some) are recursively created. Now describe FindRootPoly()
|
First UpdateStatus() - function for printing rotating dash (since creating tree can last quite long it's good to know if it's stuck or it's doing something) Next there are simple functions for classifying vertex (face) relative position to plane. Function FindRootPoly() itself counts polygons on all sides of plane and the ones to split. At the same time add results to total sums of polygons, helping to tell if node is convex (it's convex if all polygons are lying on one side and there are no splits) It actually will be convex or concave or none of that. It depends on direction we want to draw (front-to-back or back-to-front) which one we allow to skip creating next node - so it will be necessary to modify this part ! Then actual score is computed, compared with the previous one and sometimes updated. Then do rotating dash. On the end of function, convexity test is made and -1 or splitting face index is returned. This will be propably the slowest possible way to find splitting face.
I know one more method for doing that - it was invented by Paul Nettle aka. Midnight (hope i'm not wrong). The face planes are put into so called gauss map (groups, divided by normal and sorted by prependicular distance from zero) and then in each group the plane with best balance is found. (since planes are sorted, you can use quick algorithm of interval halving or another name Newton search) From these best planes the one with fewest splits is selected as splitting plane. It will be quite faster, but it assumes some faces have the same normal vector (ie. parallel planes), but when considering common quake level, most of surfaces are prependicular to itself.
But back to our algorithm. Now we're missing only PartitionSpace() :
|
On the beginning the facelists are set clear, flags is set to zero (no subnodes) and faces are subdivided into their respective facelists. At the same time, flags are updated. It's simple.
I won't tell you how does facelists work, because it's really simple aswell as file writing / loading routines. If you find something difficult, just mail me or get some book about C.
By now, we should have everything we need to write the very basic BSP-compiller. You can download source codes, compille exe and watch the spinning dash ! (when debugging my first BSP, i even dreamed about it !)



Basic BSP tree ussage
If you are keen on games, you may know that lots of games are using BSP's. But it's a bit different (but offen) way than we will do today. We will use BSP-tree for sorting surfaces in order to be drawn correctly. For example Quake, Unreal or Half-life are using precomputed visibility sets (PVS) The BSP is taken to generate convex zones. Based on spawnpoint locations (that's where player is born) select zones where player can reach. From the other ones remove all the geometry (this part is called hidden surface removal, guess why ...) Then for each zone take all possible viewing points and determine which other zones are visible from it. So when drawing, you almost exactly knows that all of the faces you draw will be visible. This is ideal, because it elliminates overdraw so we can use Z-buffer. (almost all older games (Quake I, Unreal I and Half-life I) were using S-buffer as I'm going to tell you in next part) But there is one more way to use BSP tree. For example Descent (I, II) used portal - based rendering. You generate zones again, but you don't compute PVS, but create potrals. They're areas, connecting zones so when rendering, the area (and it's contents) containing camera was drawn. Then visible portal was taken and next area was drawn recursively, but clipped by that portal's edges. This method will make zero overdraw (assuming only BSP is drawn - ie. no objects, etc ...), but it's hard to make hardware accelerated (ok, i could use stencil buffer and clipping planes, but PVS will be faster - and simpler)
Now back to our source again. So we will use it to sort surfaces. When drawing with Z-buffer, we could only check if something was drawn before (it will be more likely C - coverage buffer) and when screen is full we can stop drawing. That's not bad, but for now we will show only simple BSP traversal :
|
That was the very basic ussage of BSP. It will draw polygons back to front. If you'd like to switch the order, you will have to swap order of sub-node drawing in both branches (or invert the condition) The rest will be just like paither's algorithm : clip, transform, rasterize. I won't go deeper now since you should be able to understand that. Here is source for BSP - engine :



Positives and negatives of BSP
The certain disadvantage is polygon overdraw. Next disadvantage is that world is static. Moving things can't be part of BSP. So what did it bring us ? We can tell where camera is very fast and we can do very fast raytracing. That's all - if you have pure BSP, but when using portals or PVS, it will be significant boost. It could be also used with some algorithm for visibility determination (hardware Z-buffer or S-buffer / C-buffer) for more speed-up. Something on S-Buffer in next part ...
Variants of BSP
We just described BSP-trees, but it's not the only sort of spatial subdivision. Very common are OcTrees (Octal) - world is in cube, it will have eight sub-cubes (divided in half by x, y and z - axis) That is useful when world doesn't contain any good surfaces for splitting (for example terrain ...) There are KD-trees, they are just like BSP, but dividing planes will be always prependicular to one of coordinate axes (x, y / z).
For BSP-trees - today we used BSP - tree with onplane lists, but for PVS is used so called leaf BSP. It focuses on faces inside of node, not just onplanelists. But more on that later when writing some PVS based OpenGL engine ... bye !
Yes, people - write your opinion about pages, my terrible english ... Should i translate also comments in source codes ??
-tHE SWINe-