Czech Welcome Guff Coding 3D - Engine Guestbook Links Downloads About author Mail me Mailform
 3D Engine 10 - Lights and lighting methods 2 (stencil shadows)
3D Engine 10 - Lights and lighting methods 2 (stencil shadows) 
Hi !
So i'm sitting in front of my computer granny P 120, monstrously overclocked to 133 and looking for what could i do on it. Well, it should handle editing some text. How did you like previous part ? Shadow-buffer ? I thing it wasn't so bat although it was quite slow and non-realistic. We'll look at another technique. Which one it is can be found in topic list (or by reading on :o))
Raytracing
It's name completely describes this method. It's about tracing rays. You will propably have whole engine based on raytracing as lots of poeple does. You don't draw any polygons (so goodbye rasterizer, goodbye s-buffer !) You simply shoot rays from point where camera is located to space in camera's FOV. When ray hit some objects, you take nearest instersection (Z-Buffer analogous), determine it's color and draw it to pixel, corresponding with ray. (rays are shot to correspond with screen pixels, not chaotically) Objects aren't specified by polygons (alhough many raytracers support polygons) but by equations. So you can see raytraced spheres, planes, cones or whatever you can mathematically define.
We already know plane equation:
ax + by + cz + d = 0
and sphere would be:
(center.x - x)2 + (center.y - y)2 + (center.z - z)2 = radius2
Get that ? It's raytracing. It's not very fast, but if you add some optimizations like spacial subdivision (octrees / kd-trees) or adaptive multisampling (you trace rays in grid say 8 * 8 pixels and compare their colors. when they are similar enough, you fill entire 8 * 8 pixel area with interpolation of these four colors. If not, you do the same for this part of image only say with resolution 4 * 4 pixels) It can save quite a lot computing, especially when you compute reflections and/or refractions.
Difficult thing is to do textured objects. It's impossible uv's to infinite plane so here comes some xyz -> uv mapping techniques. You know position of point in world (and it's normal) and you should be able to compute texture coordinates. Easiest is to find greatest component of normal vector and then place texture to plane, lying on other two components. For example if x is greatest, texture will lie on yz plane (it means
But you don't have to do texture mapping at all. You can write down some formula to gain resulting color from xyz coordinates. It's called procedural texturing. Offen such procedural textures are all kinds of marbles (wood-like), noises, checkboards or stones (limestone).
Raytracing and C ++ were born for each other. You have some base class CGeometry with member functions for intersection with ray, normal in certain point, etc ... And then write all kinds of objects like CSphere, CPlane, CCone, CTorus and C ++ will handle lots of coding for you. You can also make objects, originated as boolean operations of some objects (for example cone and two spheres would form pill or two cones with different radius could form tube) simply as CBoolUnion(CGeometry *a, CGeometry *b), CBoolSubtraction(CGeometry *a, CGeometry *b) or CBoolIntersect(CGeometry *a, CGeometry *b).
In raytracing it's offen you compute reflections. How does it look then ? Great:
So i'm sitting in front of my computer granny P 120, monstrously overclocked to 133 and looking for what could i do on it. Well, it should handle editing some text. How did you like previous part ? Shadow-buffer ? I thing it wasn't so bat although it was quite slow and non-realistic. We'll look at another technique. Which one it is can be found in topic list (or by reading on :o))
Raytracing
It's name completely describes this method. It's about tracing rays. You will propably have whole engine based on raytracing as lots of poeple does. You don't draw any polygons (so goodbye rasterizer, goodbye s-buffer !) You simply shoot rays from point where camera is located to space in camera's FOV. When ray hit some objects, you take nearest instersection (Z-Buffer analogous), determine it's color and draw it to pixel, corresponding with ray. (rays are shot to correspond with screen pixels, not chaotically) Objects aren't specified by polygons (alhough many raytracers support polygons) but by equations. So you can see raytraced spheres, planes, cones or whatever you can mathematically define.
We already know plane equation:
ax + by + cz + d = 0
and sphere would be:
(center.x - x)2 + (center.y - y)2 + (center.z - z)2 = radius2
Get that ? It's raytracing. It's not very fast, but if you add some optimizations like spacial subdivision (octrees / kd-trees) or adaptive multisampling (you trace rays in grid say 8 * 8 pixels and compare their colors. when they are similar enough, you fill entire 8 * 8 pixel area with interpolation of these four colors. If not, you do the same for this part of image only say with resolution 4 * 4 pixels) It can save quite a lot computing, especially when you compute reflections and/or refractions.
Difficult thing is to do textured objects. It's impossible uv's to infinite plane so here comes some xyz -> uv mapping techniques. You know position of point in world (and it's normal) and you should be able to compute texture coordinates. Easiest is to find greatest component of normal vector and then place texture to plane, lying on other two components. For example if x is greatest, texture will lie on yz plane (it means
u = y; v = z;)
You will propably have to scale these down.But you don't have to do texture mapping at all. You can write down some formula to gain resulting color from xyz coordinates. It's called procedural texturing. Offen such procedural textures are all kinds of marbles (wood-like), noises, checkboards or stones (limestone).
Raytracing and C ++ were born for each other. You have some base class CGeometry with member functions for intersection with ray, normal in certain point, etc ... And then write all kinds of objects like CSphere, CPlane, CCone, CTorus and C ++ will handle lots of coding for you. You can also make objects, originated as boolean operations of some objects (for example cone and two spheres would form pill or two cones with different radius could form tube) simply as CBoolUnion(CGeometry *a, CGeometry *b), CBoolSubtraction(CGeometry *a, CGeometry *b) or CBoolIntersect(CGeometry *a, CGeometry *b).
In raytracing it's offen you compute reflections. How does it look then ? Great:

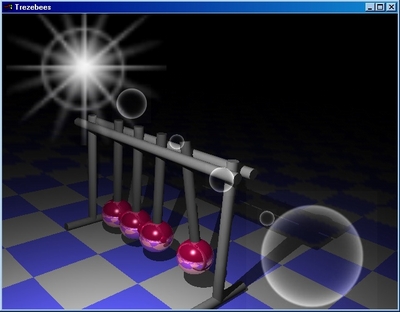
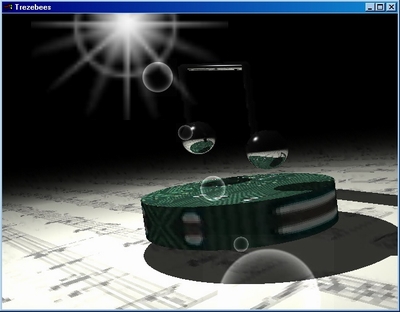
Wonderful, isn't it ?
Raycasting
Raycasting is raytracing without reflections. You simply shoot ray and determine position of nearest intersection. Then shoot rays to all lights to determine lighting values, combine with hit object color and draw. When you shoot more rays to points near the light (for example to some sphere arround light), you can have smooth shadows.
We can do something like that also with polygons. We can't afford full screen resolution (or i can't with my P 133) so it's quite enough to do half or quarter resolution and then (bilinear filtered) put it on screen. We can use some optimalizations such as bouding spheres, octrees or BSP. You don't know bounding sphere yet so i'm gonna explain it.
Bounding sphere algorithm
Bounding sphere is simply sphere, wrapping object arround. When firing ray, i check if it hits sphere (ray/sphere check is fast) till it does, then do some more expensive computing to check if ray really hit object, sphere is arround. Sphere is defined by it's center and it's radius. So, we take sphere equation and write this:
(center.x - x)2 + (center.y - y)2 + (center.z - z)2 = radius2
In case this equation is true, we have point [x, y, z], lying on sphere. (if it was below radius, point is inside sphere) But we need intersection with ray. When you imagine ray, it can be defined as some point ray goes trough and ray direction. When you put this equation with equation above, we should get quadratic equation. It can have one (ray exactly touches sphere), two (ray penetrate sphere and leave it on the other side) or no result. Solving this equation yield in coordinates. But we don't want them. We only want to know if ray hits the sphere. If you remember quadratic equations, it's number of sollution roots is dependent on discriminant. In case it's zero, we have single result in case it's positive we have two different results. We have situation:
Raycasting is raytracing without reflections. You simply shoot ray and determine position of nearest intersection. Then shoot rays to all lights to determine lighting values, combine with hit object color and draw. When you shoot more rays to points near the light (for example to some sphere arround light), you can have smooth shadows.
We can do something like that also with polygons. We can't afford full screen resolution (or i can't with my P 133) so it's quite enough to do half or quarter resolution and then (bilinear filtered) put it on screen. We can use some optimalizations such as bouding spheres, octrees or BSP. You don't know bounding sphere yet so i'm gonna explain it.
Bounding sphere algorithm
Bounding sphere is simply sphere, wrapping object arround. When firing ray, i check if it hits sphere (ray/sphere check is fast) till it does, then do some more expensive computing to check if ray really hit object, sphere is arround. Sphere is defined by it's center and it's radius. So, we take sphere equation and write this:
(center.x - x)2 + (center.y - y)2 + (center.z - z)2 = radius2
In case this equation is true, we have point [x, y, z], lying on sphere. (if it was below radius, point is inside sphere) But we need intersection with ray. When you imagine ray, it can be defined as some point ray goes trough and ray direction. When you put this equation with equation above, we should get quadratic equation. It can have one (ray exactly touches sphere), two (ray penetrate sphere and leave it on the other side) or no result. Solving this equation yield in coordinates. But we don't want them. We only want to know if ray hits the sphere. If you remember quadratic equations, it's number of sollution roots is dependent on discriminant. In case it's zero, we have single result in case it's positive we have two different results. We have situation:
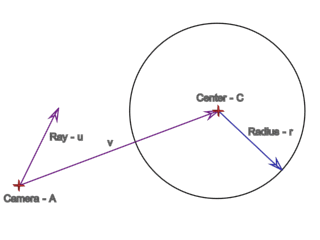
Where:
Now we need x, y and z of that equation. I'll write it down completely so math fans can celebrate:
and in the same time:
and t > 0 (we want half-ray so we won't display stuff behind camera)
And now we have equation we can extract discriminant from.
(base form of quadratic equation would be _At2 + _Bt + _C = 0)
We could derive t1 and t2:
We can make it a bit simpler by telling ray direction vector must be unit (it's length must be 1):
You should know this from school. (+- mean compute t1 with + and t2 with -). You would pass it to ray equation and would have intersection. (since square root is always pozitive - or zero, you can tell the near intersection (in ray direction) is t1 in equation above) We're interested in discriminant only:
... and when D is positive, we have intersection. Huff, it's terrible. I'll rather put this to excel and check it out. Yes, it works (on 2nd try):
There are function for computing intersection distance and other one that compute also it's coordinates.
There also one more intuitive way to do this, which you maybe weren't told in school because it's using trigonometry and planimetry together what teachers usually don't like. We have triangle - vectors u and v are lying on it's hypotenuse and adjacent side (AC). We have two points of triangle only. But we know it's rectangular (adjacent and opposite side are prependicular). We will have third point for example X. Then we can compute opposite side (XC) using goniometric functions. Then simply compare it's length with radius and we know if ray hits sphere.
r / Len(v) = tg(fi)
(fi is angle between vectors u and v)
Now we can determine if ray hit sphere but don't know how to do second part of test - object/ray intersection. We assume our objects will be polygonal:
Face - ray intersections
There are lots of methods, i'll show you two simplest ones. The first one is simpler - you bulid "fence" from planes arround polygon (it doesn't have to be necessary face, but it has to be convex) We calculate ray intersection with polygon plane and if it lies inside of that fence, we won.
A = point ray is shot from C = sphere center u = ray direction v = vector shooter point - sphere center r = sphere radius I = intersection |
Now we need x, y and z of that equation. I'll write it down completely so math fans can celebrate:
(C.x - I.x)2 + (C.y - I.y)2 + (C.z - I.z)2 = r2 |
I = A + tv (ray equation) |
and t > 0 (we want half-ray so we won't display stuff behind camera)
C.x2 - 2C.xI.x + I.x2 + C.y2 - 2C.yI.y + I.y2 + C.z2 - 2C.zI.z + I.z2 = r2 (C.x2 + C.y2 + C.z2 - r2) - 2C.xI.x + I.x2 - 2C.yI.y + I.y2 - 2C.zI.z + I.z2 = 0 I.x = (A.x + tv.x) I.y = (A.y + tv.y) I.z = (A.z + tv.z) (C.x2 + C.y2 + C.z2 - r2) - 2C.x(A.x + tv.x) + (A.x + tv.x)2 - 2C.y(A.y + tv.y) + (A.y + tv.y)2 - 2C.z(A.z + tv.z) + (A.z + tv.z)2 = 0 (C.x2 + C.y2 + C.z2 - r2) - 2C.xA.x - 2C.xtv.x + A.x2 + 2A.xtv.x + t2v.x2 - 2C.yA.y - 2C.ytv.y + A.y2 + 2A.ytv.y + t2v.y2 - 2C.zA.z - 2C.ztv.z + A.z2 + 2A.ztv.z + t2v.z2 = 0 (C.x2 + C.y2 + C.z2 - r2) - 2C.xA.x + 2tv.x(-C.x + A.x) + A.x2 + t2v.x2 - 2C.yA.y + 2tv.y(-C.y + A.y) + A.y2 + t2v.y2 - 2C.zA.z + 2tv.z(-C.z + A.z) + A.z2 + t2v.z2 = 0 (C.x2 + C.y2 + C.z2 - r2 - 2C.xA.x - 2C.yA.y - 2C.zA.z + A.x2 + A.y2 + A.z2) + 2tv.x(-C.x + A.x) + 2tv.y(-C.y + A.y) + 2tv.z(-C.z + A.z) + t2v.x2 + t2v.y2 + t2v.z2 = 0 (C.x2 + C.y2 + C.z2 - r2 - 2C.xA.x - 2C.yA.y - 2C.zA.z + A.x2 + A.y2 + A.z2) + 2t(v.x(-C.z + A.x) + v.y(-C.z + A.y) + v.z(-C.z + A.z)) + t2(v.x2 + v.y2 + v.z2) = 0 |
And now we have equation we can extract discriminant from.
(base form of quadratic equation would be _At2 + _Bt + _C = 0)
_A = v.x2 + v.y2 + v.z2 _B = 2(v.x(-C.x + A.x) + v.y(-C.y + A.y) + v.z(-C.z + A.z)) _C = (C.x2 + C.y2 + C.z2 - r2 - 2(C.xA.x + C.yA.y + C.zA.z) + A.x2 + A.y2 + A.z2) |
We could derive t1 and t2:
t1,2 = (_B +- sqrt(_B2 - 4_A_C)) / 2_A |
We can make it a bit simpler by telling ray direction vector must be unit (it's length must be 1):
q = A - C _A = v.x2 + v.y2 + v.z2 = 1 _B = 2(v.xq.x + v.yq.y + v.zq.z) = 2(v * q) _C = |C| + |A| - 2(C * A) - r2 = |q|2 - r2 t1, t2 = (_B +- sqrt(_B2 - 4_A_C)) / 2_A t1, t2 = (_B +- sqrt(_B2 - 4_C)) / 2 _B' = v * q = _B / 2 t1, t2 = (2_B' +- sqrt(4_B'2 - 4_C)) / 2 t1, t2 = (2_B' +- sqrt(4(_B'2 - _C))) / 2 t1, t2 = (2_B' +- 2sqrt(_B'2 - _C)) / 2 t1 = _B' - sqrt(_B'2 - _C) t2 = _B' + sqrt(_B'2 - _C) |
You should know this from school. (+- mean compute t1 with + and t2 with -). You would pass it to ray equation and would have intersection. (since square root is always pozitive - or zero, you can tell the near intersection (in ray direction) is t1 in equation above) We're interested in discriminant only:
D = _B2 - 4_A_C = _B'2 - _C = (v * q)2 - |q|2 + r2 |
... and when D is positive, we have intersection. Huff, it's terrible. I'll rather put this to excel and check it out. Yes, it works (on 2nd try):
|
There are function for computing intersection distance and other one that compute also it's coordinates.
There also one more intuitive way to do this, which you maybe weren't told in school because it's using trigonometry and planimetry together what teachers usually don't like. We have triangle - vectors u and v are lying on it's hypotenuse and adjacent side (AC). We have two points of triangle only. But we know it's rectangular (adjacent and opposite side are prependicular). We will have third point for example X. Then we can compute opposite side (XC) using goniometric functions. Then simply compare it's length with radius and we know if ray hits sphere.
r / Len(v) = tg(fi)
(fi is angle between vectors u and v)
Now we can determine if ray hit sphere but don't know how to do second part of test - object/ray intersection. We assume our objects will be polygonal:
Face - ray intersections
There are lots of methods, i'll show you two simplest ones. The first one is simpler - you bulid "fence" from planes arround polygon (it doesn't have to be necessary face, but it has to be convex) We calculate ray intersection with polygon plane and if it lies inside of that fence, we won.
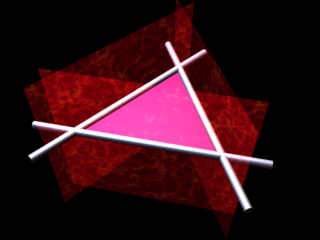
These strange looking thingies are planes
I'll show you directly resulting code, it's nothing complicated about that:
Next, more ingenious method (although not so exact) method is angle sum. Angle sum for vectors from point inside convex polygon to all it's vertices will be 180 degrees.
So we compute intersection again and then compute angles between vectors to vertices (psi1 psi2 psi3 on image). In case it's Pi (180°), face is hit. Bad is you have to put here some tollerance what causes errors.
|
Next, more ingenious method (although not so exact) method is angle sum. Angle sum for vectors from point inside convex polygon to all it's vertices will be 180 degrees.
So we compute intersection again and then compute angles between vectors to vertices (psi1 psi2 psi3 on image). In case it's Pi (180°), face is hit. Bad is you have to put here some tollerance what causes errors.
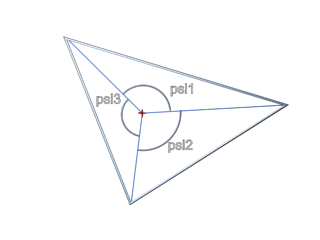
I'll put here code again:
When you want to write something really fast, use some advanced method (for example something with barycentric coordinates or so) This is just for you to understand basic principles ...
Raycasting with shadow rays
So we can write it now. We'll draw world as before, but we'll raytrace one more layer, containing light values. We'll do a bit cheating, becaues we'll use polygon id-s to speed up (we won't actually have to check for intersections, because we already know from s-buffer which polygon is nearest. you can do the same on 3d-cards reading poly-id's from frame or stencil buffer back to ram) This method is a bit outdated so i'm not going to explain it now. I'll show you how to do it with OpenGL later.
Stencil shadows
Stencil buffer is extension of all new 3D cards. Well, new is not the right word, because archaic Riva TNT actually had it (or at least i think so) It's buffer, not used for rendering but for integer operations. What does have integer buffer to do with shadows ? I'll show you, listen ..
Stencil shadows are based on shadow volumes. You project shadow polygon, going theroetically to infinity. We won't have any inifinty so we'll have to cap them (ie. draw original triangle, projected to the end of volume, facing outside of volume) Anything inside that volume is astonishingly in shadow:
|
When you want to write something really fast, use some advanced method (for example something with barycentric coordinates or so) This is just for you to understand basic principles ...
Raycasting with shadow rays
So we can write it now. We'll draw world as before, but we'll raytrace one more layer, containing light values. We'll do a bit cheating, becaues we'll use polygon id-s to speed up (we won't actually have to check for intersections, because we already know from s-buffer which polygon is nearest. you can do the same on 3d-cards reading poly-id's from frame or stencil buffer back to ram) This method is a bit outdated so i'm not going to explain it now. I'll show you how to do it with OpenGL later.
Stencil shadows
Stencil buffer is extension of all new 3D cards. Well, new is not the right word, because archaic Riva TNT actually had it (or at least i think so) It's buffer, not used for rendering but for integer operations. What does have integer buffer to do with shadows ? I'll show you, listen ..
Stencil shadows are based on shadow volumes. You project shadow polygon, going theroetically to infinity. We won't have any inifinty so we'll have to cap them (ie. draw original triangle, projected to the end of volume, facing outside of volume) Anything inside that volume is astonishingly in shadow:
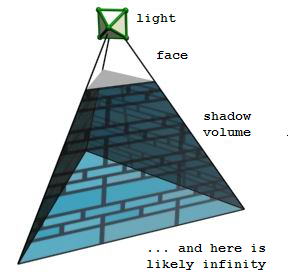
So with stencil shadows you have to render the scene with ambient light (need s(or z)-buffer of scene)
And then draw volumes to stencil buffer (you have to clear it before) When polygon of shadow volume
is facing camera, you add one to corresponding pixels in stencil, otherwise (backfacing polys)
subtract one. Now, in place where is no shadow volume or where both sides of volume are visible
you have zero value (because on the beginning of drawing there were zeros in whole buffer).
In places where only front or only back side of volume is visible, we have non-zero value.
Imagine it in your mind and you can see non-zero value mean shadows !
It's cool, because we're doing shadows in screen-space but it has one flaw. When camera gets inside of volume, you can obviously see only backfacing polygons, resulting into negative shadows or some similar error. It's not possible to check if camera is inside of volume (even when volumes were convex) - rasterizer will always produce a bit different results and scene would propably go into negative shadows when passing side of volume. We can deal with it by clipping volumes into FOV so they're always completely visible and camera never get inside geomethry. This includes pretty much of work and because we're lazy coders we'll try smarter method, invented by John Carmack which is invariant to this flaw. His original idea was to draw volumes with disabled depth-test but increment stencil for back-facing and decrement for front-facing sides of volume. Then draw volume again with testing depth and do it conversely, ie. increment for front-facing and decrement for back-facing. The result is effectively the same, but it requires one more pass. Let's see if we could improve that:
Advantage againist shadow-buffer is shadows are perfectly sharp (which can be also disadvantage). We (and noone) can filter stencil shadows (have you played Doom3 ?) I could talk about Doom 3 for a while. It uses our (Carmack's) faster method. All lights in Doom 3 are attentuated so volumes have finite lengths. In hardware you also have to set minimal and maximal draw distance (less = improved z-buffer precision) so Caramack compute distance to mos far volume/geometry and pass result. In case of Doom3's confined areas it results in quite precise z-buffer.
It can be even more optimalised (as in Doom) - you don't draw volume of each face, but you draw volume for silhouette of each object. You can display silhouettes in doom by typing "r_showSilhouette 1" into his console. Sihouette is determined from neighbouring faces (if neighbour of face isn't visible then common edge is part of silhouette) It's on picture:
It's cool, because we're doing shadows in screen-space but it has one flaw. When camera gets inside of volume, you can obviously see only backfacing polygons, resulting into negative shadows or some similar error. It's not possible to check if camera is inside of volume (even when volumes were convex) - rasterizer will always produce a bit different results and scene would propably go into negative shadows when passing side of volume. We can deal with it by clipping volumes into FOV so they're always completely visible and camera never get inside geomethry. This includes pretty much of work and because we're lazy coders we'll try smarter method, invented by John Carmack which is invariant to this flaw. His original idea was to draw volumes with disabled depth-test but increment stencil for back-facing and decrement for front-facing sides of volume. Then draw volume again with testing depth and do it conversely, ie. increment for front-facing and decrement for back-facing. The result is effectively the same, but it requires one more pass. Let's see if we could improve that:
- front-facing, always decrement
- back-facing, always increment
- front-facing, if visible (depth pass) - increment
- back-facing, depth pass - decrement
- front-facing, depth fail - decrement
- back-facing, depth fail - increment
Advantage againist shadow-buffer is shadows are perfectly sharp (which can be also disadvantage). We (and noone) can filter stencil shadows (have you played Doom3 ?) I could talk about Doom 3 for a while. It uses our (Carmack's) faster method. All lights in Doom 3 are attentuated so volumes have finite lengths. In hardware you also have to set minimal and maximal draw distance (less = improved z-buffer precision) so Caramack compute distance to mos far volume/geometry and pass result. In case of Doom3's confined areas it results in quite precise z-buffer.
It can be even more optimalised (as in Doom) - you don't draw volume of each face, but you draw volume for silhouette of each object. You can display silhouettes in doom by typing "r_showSilhouette 1" into his console. Sihouette is determined from neighbouring faces (if neighbour of face isn't visible then common edge is part of silhouette) It's on picture:
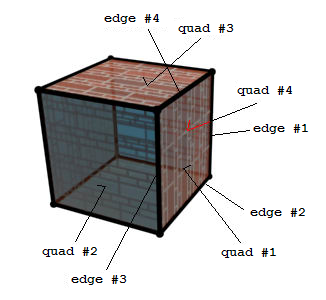
We'll now determine which edges of box are part of silhouette. Imagine this cube is from
view of light (in stencil we have no views of light, all lights are omni, but we can put camera
into light position and look at cube, right ?) We'll check quad 1. It's visible so it's facing light.
Now we have four edges, one of them (edge #1) is shared with quad 4. Quad 4 isn't visible so we have
first edge of silhouette. The same pay for edge #2. But edges #3 and #4 are shared with quads 2
and 3 which are visible so they won't come into silhouette. When you do this with every face,
you'll have complete enclosed silhouette of object. Now we should project it. In complex objects,
silhouette is quite strange when viewing from another view than light-view, because vertices
of object are in different distance from light. We should project them so their projections
are all in the same distance from light (in order to handle finite volumes nicely)

silhouettes in our scene
One more thing - you have to cap volumes. You have to cap both front and back (projected) end. It's done by drawing front-facing and projected backfacing part of object. Again - make all vertices same distance from light. It will then look nicely, but you have to count on large polygons with light above it's centre. Volume will then have to be projected more far from light in order to generate correct shadows. (I hope you understand better with this picture)

big table shadow poly is nearer than the others
Now it should be no problem to write example so i'll try it. Please wait.
At the end i solved it with two routines, because s-buffer really bad handles coplanar surfaces so i'm drawing whole volume without depth test and then (without front side - which is coplanar with original faces and that resulted in incredible blinking of whole screen. Maybe later with z-buffer) I also (speed purposes) left out drawing far volume caps because they're never visible when inside room (in example there's room with some chairs), but when you fly outside of the room, you'll see entire scene in shadow.
So the entire difficulity is find neighbouring faces:
|
Function b_SameVertex() is for determining if vertices lies in the same place (there can be more vertices in the same place with diffferent texture coords). In function Find_FaceNeighbours() first set neighbours for each face to NULL and then take all faces and check if there's same edge.
Something more to light. In example is 3ds world with one light which is moved in circle arround it's original position. After drawing stencil we take image and divide shadowed parts of it by 2 (make it half bright or twice dark if you wish) That's absolutely crazy sollution (again). You should draw scene with ambient lighting and with each stencil pass add diffuse and specular colors for each light in scene (we have support for infinite number of lights).
Download your example and see you later !



Next tutorial is going to be about lightmaps ...
Wait wait wait ! I'm translating this tutorial and i'm a bit ashamed for it. I'm going to write it a bit differently in order to have correct shadows using second method and also include some shading model...
Wait wait wait ! I'm translating this tutorial and i'm a bit ashamed for it. I'm going to write it a bit differently in order to have correct shadows using second method and also include some shading model...



.. and here it comes ! It uses smooth shading and enhanced shadow generation algorithm so it's almost twice as fast as previous one. Enjoy !
-tHE SWINe-
-tHE SWINe-